A client looking to save money on energy expenses replaced their conventional thermostat with a smart one. The goal was to reduce energy bills by making efficiency gains. When significant reduction in energy expenditure failed to materialize, the client reached out to Midnight Mechanism for analysis from first principles. An overview of the client’s system immediately follows.
Overview
An acceptable indoor temperature range of 62°F to 77°F was established, with an optimum setpoint of 68°F. The logical flow of the program was laid out below. In the following diagram, blue signifies that the cooling system was on whereas red indicates that the heating system was on, with $T(in)$ and $T(out)$ representing indoor and outdoor temperatures, respectively.
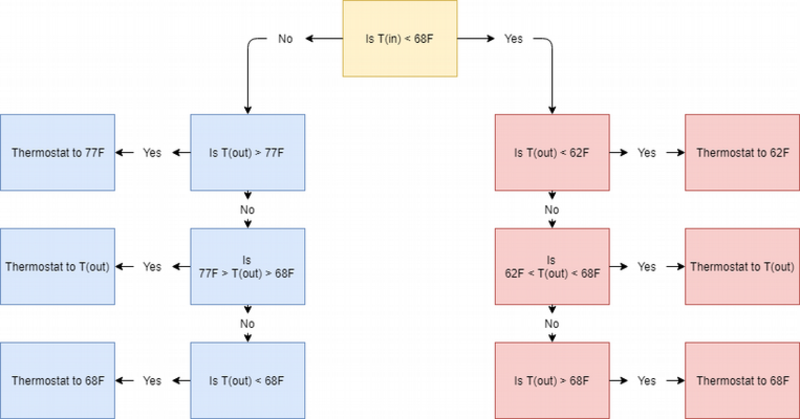
Fig. 1: Smart thermostat logic
This system incorporates outdoor temperature in an effort to reduce energy consumption and was designed such that the client would neither have to switch between heating and cooling modes nor change the thermostat manually at night.
Analysis
The temperature and fan data shown in figures 2 and 3 below were recorded for a 24-hour period. Notice how the setpoint temperatures, indicated by the orange line, updated every time the outdoor temperature changed over its functional range.
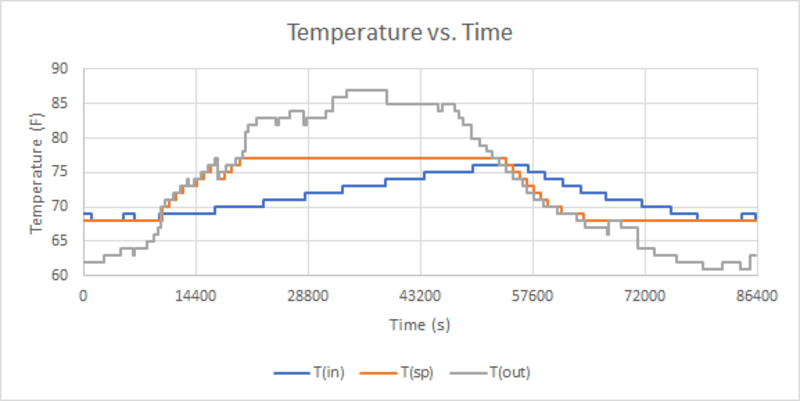
Fig. 2: Indoor, outdoor, and Setpoint Temperatures for a 24-hour period
Fan activity, corresponding to the aforementioned temperature data, immediately follows:
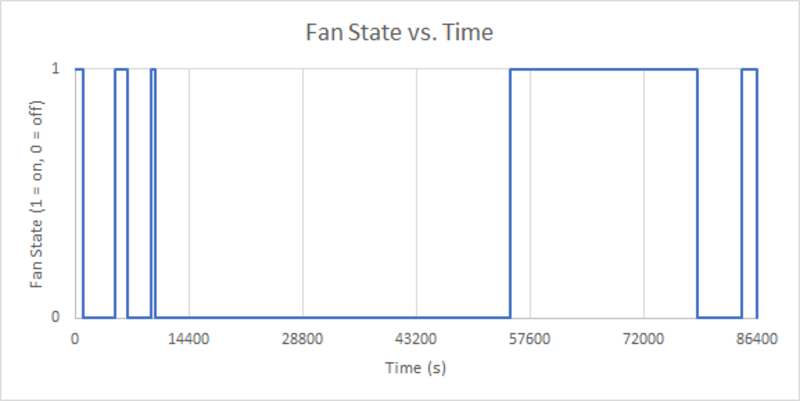
Fig. 3: Air conditioner fan statuses for 24-hour Period
The bulk of the cooling was done during late afternoon and evening. The fan also activated intermittently at night to counteract the residual heat trapped by the walls of the house during the day. With the smart thermostat, total run time for the fan was 7.98 hours, with a mean indoor temperature of 71.4°F. In order to approximate the behavior of a fan driven by a conventional thermostat with a 71.4°F setpoint, a fan-status graph was simulated where the fan was prompted to run every time $T(out)$ > 71°F:
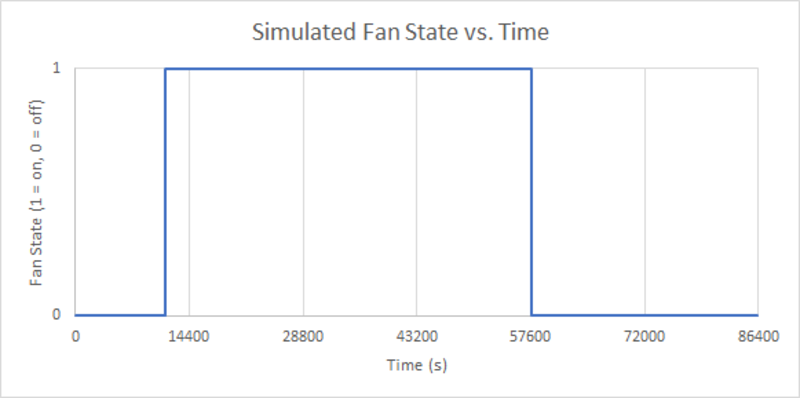
Fig. 4: Simulated air conditioner fan statuses for the same 24-hour period. Data was rounded to the nearest integer)
Total run time in the simulated scenario was 12.87 hours, which was approximately 60% longer than the run time of the fan driven by the smart thermostat. However, this was a worst-case scenario, as buildings have a moderating effect on daily temperatures, both heating and cooling more slowly than the outdoor temperatures.
The following graph utilized a sinusoidal temperature model to fit indoor and outdoor data when the AC fan was off. The periods were both fixed at 24 hours, and the mean indoor temperature was fixed to the mean outdoor temperature over the period:
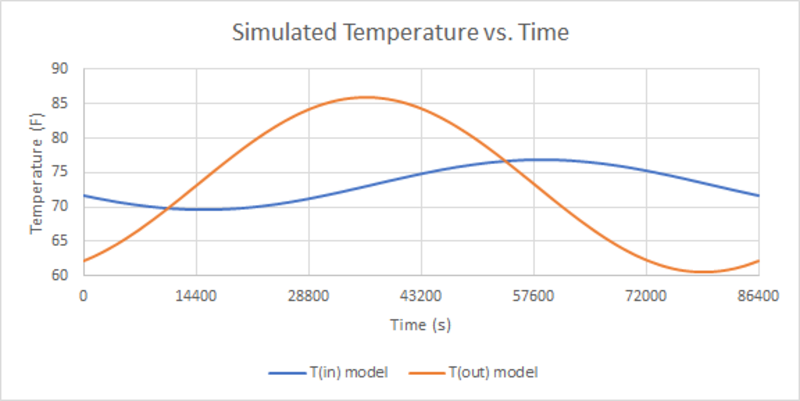
Fig. 5: Indoor and outdoor temperature model. Inside temperatures appear in blue; outside temperatures appear in orange.
The means for both models were 73.26°F, meaning that the system had a projected aggregate cooling effect of almost 2°F over the course of the 24-hour period (71.4°F). Fluctuations of indoor temperature were markedly smaller with the smart thermostat, and there was also a larger latency between extremes of indoor temperatures. In terms of comfort, the client’s smart thermostat represented a significant upgrade. In terms of efficiency, the results were more complicated.
When the outside air cools below a traditional thermostat’s set point, the thermostat ignores it, considering only internal temperature. When the outdoor air cools below a smart thermostat’s set point, the smart thermostat should trigger smart fans to intake the cooler outdoor air; therein lies the problem. Our client’s system failed to exploit the differences between internal temperatures and outside air. The AC was being used to cool the internal air instead of merely replacing the hot air with cold air. Essentially, the cool outdoor air was not being used as a heat sink.
Conclusion
Unfortunately, smart doesn’t always equal savings, as a crucial component was missing. In light of this analysis, the client plans to install smart vents and fans to take advantage of the natural heat sink caused by nightly outdoor temperatures. Sometimes the optimal strategy isn’t evident from available data; in this scenario, a novel approach was required.